
OBJETIVOS
Estudiar la aplicabilidad de las técnicas de estadística espacial sobre campimetrías visuales.
Comprobar de manera estadística la existencia de relaciones espaciales en las campimetrías visuales.
Desarrollar modelos interpolativos espaciales que permitan cuantificar las relaciones entre los puntos de una campimetría.
Análisis espacial de campimetrías visuales
de pacientes oculares
ESTADÍSTICA ESPACIAL
R
CAMPIMETRÍA VISUAL
AUTOCORRELACIÓN ESPACIAL
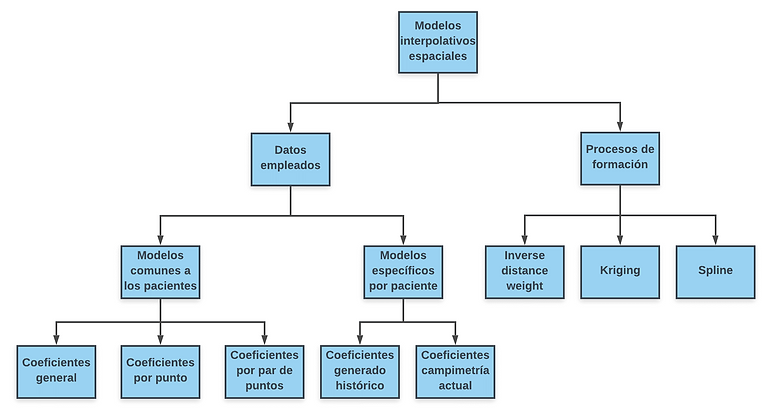
MODELOS INTERPOLATIVOS
KRIGING
SPLINE
IDW
METODOLOGÍA
Pre-procesado y limpieza de datos disponibles.
Implementación de una librería sobre R que permita la aplicación de las técnicas de la estadística espacial sobre campimetrías visuales.
Comprobación de la existencia relaciones espaciales mediante índices de autocorrelación espacial.
Desarrollo de modelos interpolativos espaciales que cuantifiquen las relaciones entre los puntos de una campimetría.
Adaptación sistemas interpolativos al histórico de cada paciente.
INTRODUCCIÓN
Una campimetría visual es una prueba diagnóstica que permite evaluar el campo de visión de un paciente. En particular, la prueba consiste en someter a distintas zonas del ojo a una serie de impulsos lumínicos de diferente intensidad, de forma que el paciente indique cuáles puede ver y cuáles no. Con esto se formaría un mapa de su campo de visión.
Esta prueba es usada asiduamente por los oftalmólogos como herramienta para llevar a cabo el diagnóstico y seguimiento de distintas afecciones oculares especialmente el glaucoma, la principal causa de ceguera en el mundo. Existe una amplia bibliografía acerca del análisis estadístico de campimetrías, sobre todo para la detección del glaucoma. Sin embargo, en estos análisis no suele emplearse la redundancia espacial contenida en las campimetrías o únicamente se hace mediante modelos muy básicos basados en la adyacencia.


El objetivo de este proyecto es emplear la estadística espacial para poder aprovechar en mayor medida la información contenida las campimetrías oculares. Más concretamente, en primera instancia se buscará confirmar de manera estadística la existencia de relaciones espaciales en las campimetrías.
En segundo lugar, se buscará proponer una serie de modelos interpolativos espaciales y analizar cuál es el que captura en mayor medida las relaciones existentes entre los puntos de la campimetría. De estos modelos se extraerá una matriz de pesos que cuantifique estas relaciones espaciales. Esta matriz podrá ser empleada para mejorar la calidad y la velocidad de los campímetros actuales además de como herramienta de apoyo para la generación de modelos espacio-temporales.
Para la realización de este proyecto se dispone de un total de 3.271 campimetrías de más de 200 pacientes diferentes, lo que se correspondería con 192.989 puntos evaluados, tomadas entre los años 2003 y 2018. Estas campimetrías han sido proporcionadas por el servicio de oftalmología del Hospital Clínico San Carlos, Madrid.
DESARROLLO
Para evaluar la existencia de relaciones con el vecindario se han empleado dos de los principales índices de autocorrelación espacial, como son el índice de Moran y el coeficiente de Geary. Basándose en estos dos se han realizado una serie de simulaciones de Montecarlo para confirmar la presencia de estas relaciones. Asimismo, durante el análisis preliminar también se ha explorado la distribución temporal entre muestras tomadas y posibles transformaciones de utilidad a la hora de representar y sintetizar la información disponible.
De cara a representar las relaciones espaciales existentes en una campimetría se han propuesto varias alternativas de modelos interpolativos espaciales. El primero de estos tipos está formado por diferentes estructuras que se basan en generar el semivariograma asociado al conjunto de campimetrías disponibles y ajustar modelos de regresión que expliquen la varianza vista en este en base a la distancia que separa cada par de puntos.
A partir de estos modelos de regresión se podría calcular una matriz de ponderaciones que almacenase las relaciones entre cada par de puntos de la campimetría. Esta matriz sería la empleada para llevar a cabo las interpolaciones. Este procedimiento se es conocido como Kriging. En concreto, se han estudiado cuatro de las alternativas regresión más extendidas en el análisis espacial: la lineal, logarítmica, exponencial y esférica, caracterizadas cada una de ellas por el sistema que tratan de ajustar a la nube de puntos del semivariograma.
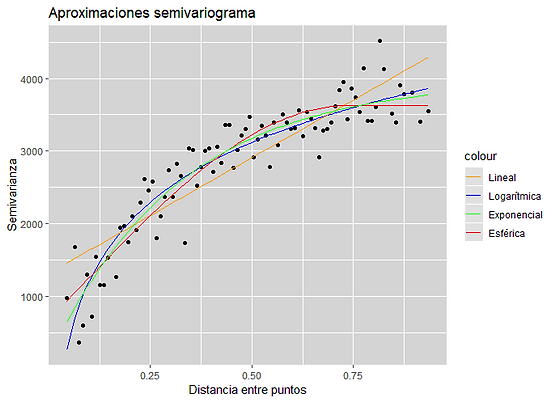
Asimismo, también se ha considerado la utilidad de sistemas interpolativos que ajusten el semivariograma a nivel de punto, es decir, que generen un semivariograma diferente para cada uno de los puntos evaluados y ajusten un modelo diferente para cada uno de ellos. Esto permite que el modelado de la distancia no sea común a todos los puntos, sino que pueda variar de unos a otros.
Además de los casos anteriores, se ha propuesto el uso de modelos que consideren individualmente las relaciones entre cada par de puntos, incrementando significativamente los patrones de variación con la distancia que pueden expresar. Junto con estos también se ha analizado un modelo de pesos inverso a la distancia (idw), que otorga un peso que decae exponencialmente con la distancia con un factor de atenuamiento entrenable.

Uno de los puntos clave a la hora de ajustar este tipo de modelos basados en el histórico del paciente es el tamaño de la ventana temporal considerada para generar el variograma. Dado que uno de los objetivos principales de este proyecto es buscar modelos que sean aplicables para la mayor cantidad posible de pacientes, se han analizado diversos tamaños de ventana para determinar cuando la adición de nuevo histórico no resulta relevante.

Dado que el uso de técnicas de análisis espacial está especialmente diseñado para datos que se distribuyen sobre una única topografía, la aplicación de librerías convencionales vuelve el procesado de las campimetrías extremadamente lento e ineficiente. Por este motivo, se ha desarrollado una librería sobre R que permite, de manera eficiente, la aplicación de las técnicas de estadística espacial sobre datos que se distribuyen sobre réplicas independientes de la misma topografía. Como consecuencia los métodos teóricos tradicionales han tenido que ser adaptados al problema en cuestión, manteniendo eso sí los conceptos elementales de la estadística espacial.
RESULTADOS
Como resultado de este proyecto se ha comprobado de manera estadística la existencia de relaciones espaciales entre los puntos de una campimetría. Además, se han propuesto e implementado diferentes modelos para representar esta redundancia espacial, obteniéndose una matriz de pesos capaz de capturar gran cantidad de estas relaciones entre los puntos de la campimetría.
A continuación, se muestran algunos ejemplos de las relaciones espaciales capturadas y como estas no están estrictamente determinadas por la adyacencia directa y la distancia entre los puntos como se considera en la bibliografía tradicional.


El segundo tipo de modelos interpolativos es similar a los previos, con la salvedad de que mientras que en los anteriores el semivariograma se generaba a partir del total de campimetrías del conjunto de entrenamiento, en estos casos es generado a partir del propio histórico del paciente. Como resultado, mientras que en los casos anteriores la matriz de ponderaciones entre puntos era igual para todas las campimetrías, en este tipo esta matriz varía entre unos pacientes y otros dependiendo de sus pruebas pasadas. Adicionalmente, también se ha considerado el funcionamiento combinado de varias de las alternativas anteriormente propuestas.